Hash, IndexOf, Lookup, Performance, Search, Sorted, String
As a followup to the previous String Lookup: Hash, Sorted or Unsorted here is a look at what happens for longer strings.
When the string you’re searching have more than a dozen characters, and you only have a few hundreds of them, a clear winner emerges.
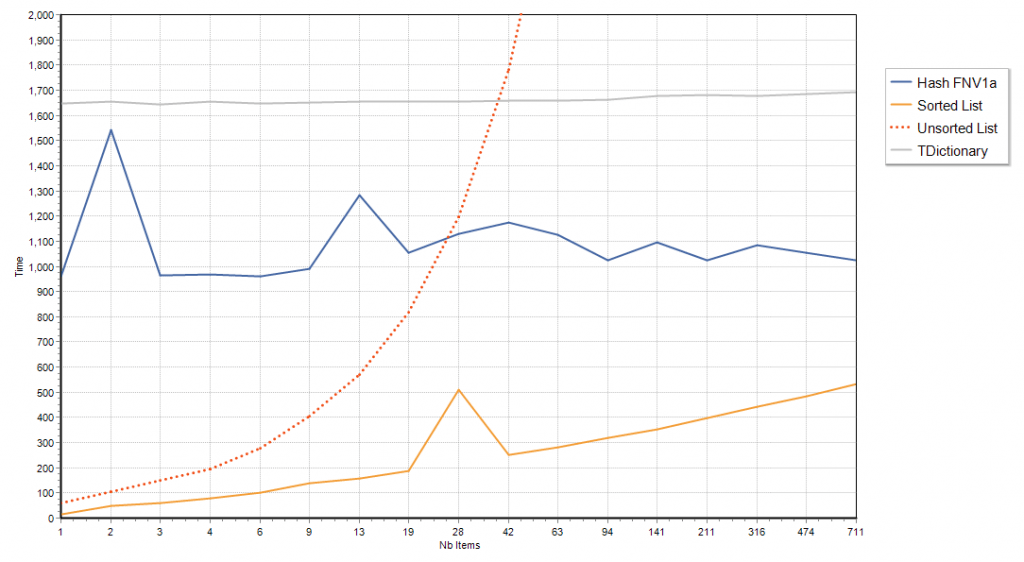
First chart is for searching strings of length 250, where the first 128 characters are ‘a’ and the rest is random.
These similar characters at the start form a of handicap for string comparisons as 128 characters will have to be looked up before the comparisons can have a chance to be decided. This is penalizing the Unsorted and Sorted list cases, as these rely solely on comparisons.
(sorry the chart is a bit noisy, I did not run too many iterations)
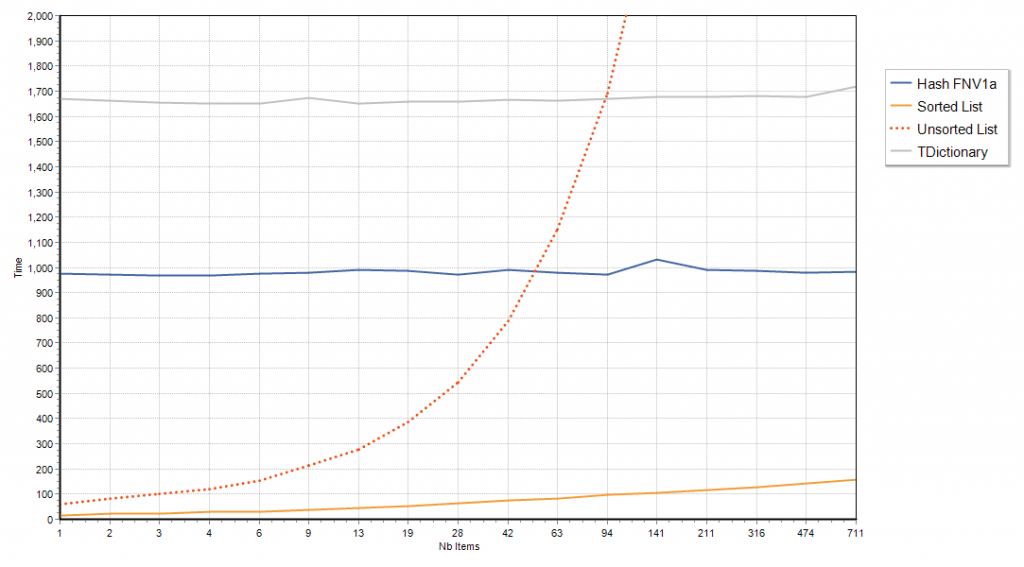
Without the handicap, if the long string characters are purely random, well, the verdict is clear
For long strings, the cost of computing the hash-code makes both hash maps implementations non-competitive, unless you have a bazillion of long strings, and a humble sorted TStringList (with CompareStrings method overridden to case-insenstive) is having a field day.
The overhead of computing the hash code is so significant, that up to a few dozen strings, even an unsorted TStringList will outperform TDictionary.
Interestingly enough, what is true for long string hash code computation will also be true for long objects (or records) hash code computations. So if your keys are large enough, and you do not have an awful lot if items, chances are a hash map will not be a very effective solution.
Strategies such as caching the hash code could help, but only if an hash code is going to be reused “enough times” to pay for its initial computation cost.
Of course hash maps have other advantages, such as being able to add and remove items cheaply (while it can be expensive in a sorted list), but raw search/lookup performance is not always going to be a given.
Would be interesting to see this test with different Hash table implementations. Should just collect few publicly available implementations, and see who wins the race 😉
This does not take into account the fact that filling the list takes also time, if you can’t sort list after it is already populated I think it becomes quite costly (Hash Table has an cost also for sure),.
@Tommi hash table implementation details do not really matter: the hash code computation costs dwarves everything else… FNV1a here is one of the faster hashes, it can be edged by CRC32, but that won’t make a lot of difference, especially for the random strings test.
And yes, hashes have other advantages when adding/removing, but while a basic sorted list will be slow adding/removing, a binary tree won’t, and will have the same performance profile for searches.
The point is that a hash table is not always the fastest or best solution around. It can sometimes be a very poor choice.
No matter how perfect the hammer, it won’t beat a screwdriver when it comes to driving screws 😉
Very nice Eric, I enjoyed this post very much.
I asked you yesterday for the code to test this because, in a real application, I save (cache) the most used queries using SQL text as key, the prepared statements, aka
ADOQuery.Preparedgreatly increases performance for multiple executions and when I firstly implemented I wondered if hashing the SQL would’nt be better than comparing the plain SQL.Of course the problem with hashes and long strings is the time it takes to compute the hash. A hybrid approach, where the hash is calculated only for part of the string (preferably a part that is different, if it is known which part that is, e.g. 8 characters starting at position 128) and the resulting collisions are resolved by sorted lists could vastly improve the performance in this case.
@Thomas that means you need to inject knowledge and make assumptions, so your code becomes case-specific, and thus fragile/non-reusable. There is nothing case-specific about a sorted TStringList, or a binary tree/search in general.
I suspect a B-tree (sort of a generalized binary tree) would be able to beat hash-based approaches whenever the data to be hashed is not short or a hash is not already available (pre-computed).
Nice readings, thank you!
It is interesting to know, what would be the best solution to store and search a list of 300 000 words of natural language, ANSI, up to 30 chars length. In terms of a memory consumption and a search speed.
I’ve tried an indexed TkbmMemoryTable, and it works pretty well. It used optimized TLists internally. But memory tables is an universal solution for data manipulations. I’m sure it’s possible to save more memory etc. May be there is an optimized Delphi library for the task?
@Kryvich With 300,000 relatively short words, hash maps should behave just fine and faster than binary search.
Though if you want the utmost speed, I suspect a B-Tree could be even faster, as it will perform at worse 30 operations (1 per character), while a hash map will perform 60 (30 for hashing, then 30 for checking the match).
If you can prep a realistic benchmark on your case, you could start a competition, there may be more creative solutions 🙂
Eric, yes, B-Tree is a good thing. When I needed to extract all word forms from the huge OCRed library, I used a homemade B-Tree for processing. As a result, after a week or two I got a list of almost 15 mln Russian language words + some usage statistics for every word. My 32-bit utility was not very optimized internally and eat 800 Mb of RAM. So this class impossible to reuse in other 32-bit applications. It’s why I ask Delphiers for better solutions.
I like this kind of post because, like Raymond Chen use to say: “Good advice comes with a rationale so you can tell when it becomes bad advice.”
What about half step? Wouldn’t it be better on sortet string lists?
@Otto what do you mean by “half step”?