
In another comment of the Curiouser Case, Arnaud Bouchez pointed to an interesting optimization that is use in mORMot‘s UpperCopy255Buf function: a branchless parallel upper case conversion.
At the core of that implementation are the following lines of code
c := src[i]; d := c or _80; dest[i] := c - ((d - _61) and not (d - _7b)) and ((not c) and _80) shr 2;
Ok, it may not be too obvious what happens at first sight. Let’s break it down.
The Magic Constants
Let’s start with the pseudo-constants, those _61, _7b and _80. They hold multiple times the byte $61, $7b and $80 respectively, as the code converts multiple characters at once. For the purpose of explaining what happen, we can focus on a single byte.
Why did I call them “pseudo-constants”? Well, they are semantically constants, but in UpperCopy255Buf they are declared as variables. This is done to have the compile will hold them in registers, which makes the code slightly smaller and reduces the number of memory accesses.
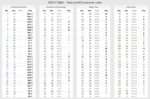 As to what thos values mean, well, let’s check the ASCII Table:
As to what thos values mean, well, let’s check the ASCII Table:
- $61 is the ‘a’ character
- $7b is the ‘{‘ character, which is just after the ‘z’ character
- $80 is a mask to the one unused bit for ASCII characters
Down the Rabbit Hole
The first line fetches a character (or a bunch of character, but let’s work with just one) and stores it into c, then the line
d := c or _80;
places into d the value of c with the upper bit forced to one. This upper bit is used as a Boolean for the rest of the snippet. You can think of d as being a bit-packed version [ bool, 7bits_ascii_code ]. So that line set the bool to true.
Next line is complex, so let’s break it into bite-sized portions:
(d - _61)
remember that d holds [ true=1, ascii_code ], its numeric value is $80 + ascii_code, so what happens is:
- if the code is equal to or above ‘a’ ($61) in the ASCII table, the result will be still be above $80, the bool is still true
- if the code is below ‘a’ in the ASCII table, the result will be lower than $80, the bool will be false
This line does a comparison with ‘a’, and the bool (upper bit) contains “true” is the character is a or above, and false otherwise. It’s performing a c >= ‘a’
Take some more tea
The next portion is
not (d – _7b)
which is thus literally equivalent to (not (c >= (character after ‘z’)) which can be simplified as c <= ‘z’, then both tests are combined with an and, so the whole snippet
((d - _61) and not (d - _7b))
is actually performing
c in ['a' .. 'z']
with the Boolean result in the upper bit. That’s the first logic portion completed. Onto the next:
((not c) and _80)
Here we invert the bits of c, and mask it with $80. For an ASCII character, the upper bit of c is zero, invert it gives us 1, which the and preserves. And if c wasn’t an ASCII character ? then the upper bit is 1, inverting it gives us a zero, and the and doesn’t change that. So this expression is actually performing:
IsCharacterASCII(c)
and placing the resulting Boolean in the upper bit! all the lower bits are zeroed.
Ah, That’s the Great Puzzle
Ok lets put almost everything together, we have an equivalent to
if (c in ['a'..'z']) and IsCharacterASCII(c) then $80 else $00
You’re still following? Let’s tackle the bite: the shr 2 is applied on that outcome. Shifting right twice is like dividing by 4, so the resulting values become just $20 and $00. The expression subtracts that to the character code c.
Now we can really put it together:
c := src[i] if (c in ['a'..'z']) and IsCharacterASCII(c) then dest[i] := c - $20 else dest[i] := c
If you read the previous article, subtracting $20 from an ASCII code when you’re in the “lower case” column of the ASCII table moves you to the “upper case” column of the ACSII table.
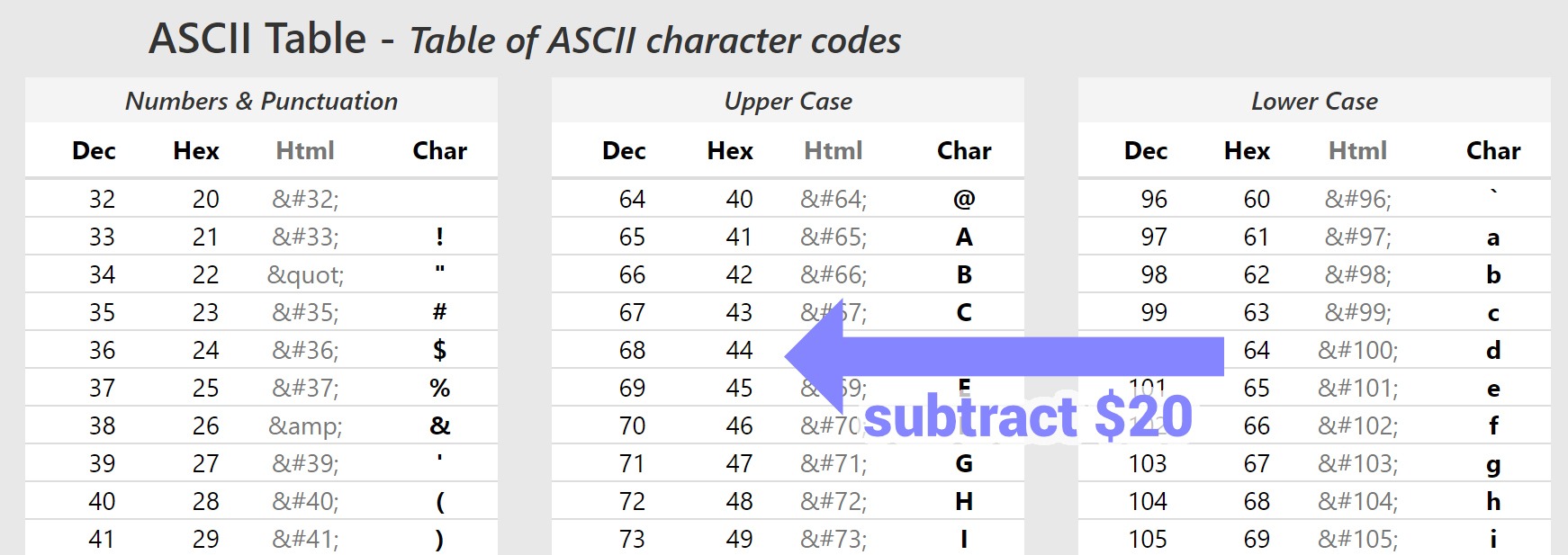
Subtracting $20 per character sounds like a good deal, but other people prefer to lower case, as it adds $20, which feels nicer if you’re looking at it from a benefits point of view.
Here we Must Run as Fast as we Can
It is branchless, but is it fast ?
When doing it on a single character, not really. It’s about 30% slower than using a branched version: the overhead of branchless computation is not enough to offset branch misprediction.
But, it can operate on multiple characters at once… And it can even be implemented with heavy vectorization in AVX, at which point it becomes memory bound. Which means on a large enough string, it will run as fast as is possible!
However, the key constraint is that operates only on ASCII. While the expression has a protection to avoid savaging Unicode characters, it won’t upper case an accented character or non-latin letter like π.



Thanks for cutting down this algorithm from the 80s. 😉
Back to the future!