In the previous episode, it appeared that Delphi XE2 64bit compiler was achieving quite good results, however, after further investigations, things may not be so clear-cut. Transcendental maths, which will be food for a another post, the subject of this one seems to be an issue with single-precision floating point maths.
edit: it appeared there is an undocumented {$EXCESSPRECISION OFF} directive which controls the generation of the conversion opcodes hampering single-precisions floating point performance, the articles has been updated. Thanks Allen Bauer, Andreano Lanusse & Leif Uneus for bringing it to attention!
Single precision
Single precision having a smaller memory footprint and being typically processed faster (especially when using SIMD, f.i. SSE allows processing 4 single-precision floats at the same time, while you can process only 2 double-precision floats at a time with SSE2), thus it is often encountered in performance-critical code where precision isn’t essential. One typical such use is for 3D computations, meshes, and geometry.
Most 3D engines out there make heavy use of single-precision floating point (GLScene and thus FireMonkey too), and it’s the primary native float data type expected by most graphics hardware.
Updated benchmark charts
However, the new 64bit compiler doesn’t like single precision floats, while the 32bit compiler likes them, this leads to this interesting chart:
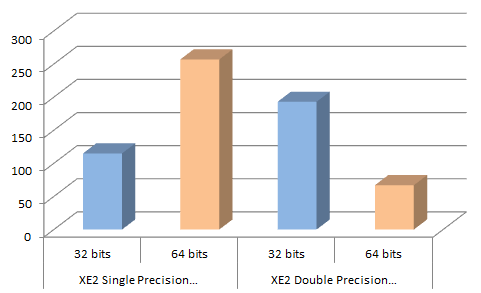
Mandelbrot times (ms), lower is better
| XE2 – 32 bits | XE2 – 64 bits | |
|---|---|---|
| Single Precision… | 115 | 257 / 66* |
| Double Precision… | 193 | 67 |
There are two figures in the 64bit single precision case, the high figure is what you see if you just compile with optimizations (yes, you’re seeing this right, single precision floating point math in Delphi 64bit behaves worse than double-precision maths in Delphi 32bits!), and the low figure is if you use the undocumented (up until this article) {$EXCESSPRECISION OFF} directive.
The new XE 64bit compiler can give you the best, and the worst: using single precision floats can make your 64 bits code almost 4 times slower if you don’t turn off “excess precision”, while it can make 32 bits code 70% faster…
Why, oh why?
The reason? The 64bit compiler doesn’t use scalar single precision opcodes if you don’t have “excess precision”, turned off and converts everything back and forth to double precision. Here is a snippet from the CPU view:
FMandelTest.pas.193: x := x0 * x0 - y0 * y0 + p; 00000000005A1468 F3480F5AC4 cvtss2sd xmm0,xmm4 00000000005A146D F3480F5ACC cvtss2sd xmm1,xmm4 00000000005A1472 F20F59C1 mulsd xmm0,xmm1 00000000005A1476 F3480F5ACD cvtss2sd xmm1,xmm5 00000000005A147B F34C0F5AC5 cvtss2sd xmm8,xmm5 00000000005A1480 F2410F59C8 mulsd xmm1,xmm8 00000000005A1485 F20F5CC1 subsd xmm0,xmm1 00000000005A1489 F3480F5ACA cvtss2sd xmm1,xmm2 00000000005A148E F20F58C1 addsd xmm0,xmm1 00000000005A1492 F2480F5AC0 cvtsd2ss xmm0,xmm0
This is the similar code as for double precision, with loads of cvtss2sd & cvtsd2ss instructions thrown in! No mulss, subss or addss in sight, and yes, you can see redundant stuff happening, 4 lines are doing the actual computation, 6 are doing conversions, and doing them every… single… time.
If you’re a fan of “Lucky Luke“, the first two lines may remind you of a Dalton brothers prison break (even though the brothers are in the same cell, they each dig their own hole to freedom) 😉
Now if you have the {$EXCESSPRECISION OFF} directive, you see a different picture, the compiler uses single-precision opcodes as expected:
FMandelTest.pas.194: x := x0 * x0 - y0 * y0 + p; 00000000005A1450 0F28C4 movaps xmm0,xmm4 00000000005A1453 F30F59C4 mulss xmm0,xmm4 00000000005A1457 0F28CD movaps xmm1,xmm5 00000000005A145A F30F59CD mulss xmm1,xmm5 00000000005A145E F30F5CC1 subss xmm0,xmm1 00000000005A1462 F30F58C2 addss xmm0,xmm2
As Ville Krumlinde pointed in the comments, VS 2010 C-compiler has the same weird behavior.
I say weird, because if you go to the length of specifying single precision floating point, it’s usually because you mean it, and it’s trivial enough to have an expression be automatically promoted to double-precision by throwing in a Double operand or cast.
This reminds me of the old $STRINGCHECKS directive, which one had to remember to adjust or suffer lower string performance. Hopefully the hand holding will be reversed in the next version, with excess precision being off by default.

Does this mean – simply use double? (Requires more memory then).
This means if you need heavy computation, use C++, the Delphi team has proven that they can’t make a decent optimizing compiler even after all this years, they’re still stuck on old Pentiums, you should check the integer benchmark (MD5, …) the compiler is really slow compared to C++ (VCC, GCC) and I mean SLOW!
Eric,
this may be out of scope, but I would like to see a comparison Delphi vs. C#/.Net – any chance to get this?
The it converts x0 twice in a expression like “x0*x0” looks particularly clumsy.
Another example:
var
s1 : single;
s1 := s1*1;
This generates conversions from single to double and then back to single again (without any multiplication because the compiler has figured out that multiply with 1.0 is unnecessary 🙂 ).
Yes, and if you pass doubles to hardware via OpenGL or DirectX, you’ll likely face a downconversion to single and an hidden buffer (ie. up to triple memory use…). Also it is not possible for direct buffering techniques, so using doubles isn’t really a solution…
@Eric
Thank you very much. This is not so good because one has to be very careful when thinking about the scenario applied to and cannot simply rely on a speedup.
@DEV…especially when someone is skilled enough to combine .net and manged C/C++ for example. ‘For the Files’: Sequence is still faster in a hand optimized C code in sequence. Currently experimenting on the client side (don’t do this on the server side) with a threading model on Windows 7 that should work now in VS2011 C/C++ that allows a ‘batch execute’ a burst controlled by a worker – on one hand controlled by the developer and on the other hand by the OS in order to hinder the worker from consuming > 80% CPU time (avoid context switches between competing ‘processes’). (can be found in the last MSDN – nothing magic but had problems in the past when cleaning up after the calculation was done). I fear such things … who knows what tomorrow will bring.
I did not expect this from Delphi … but I am little sad to hear what Eric found out.
That is disappointing..
for heavy math, we use MtxVec, from dewresearch, they use the assembly code from Intel, with SSE2, 3, 4, whatever, with a new OpenCL library that uses the GPU on FireMonkey; it’s not very easy to implement but, if you need speed, it’s the best choice I could find (I’m talking about engineering calculations that take more than 1 hour on a new i5 quad-core).
I posted this issue to the Embarcadero forums. Dalija Prasnikar asked me to create a QC entry.
Eric: Shall I create an entry about this issue?
Please do, QC is for all practical purposes unreachable from here.
Try the test again with {$EXCESSPRECISION OFF}. That will tell the compiler to use single-precision instructions, which means that intermediate results could loose precision, but that’s what you’re expecting in this case. Also, make sure you set $O+ and that will improve it further.
I just saw a comment from a compiler guy at EMB.
Setting a compiler switch $EXCESSPRECISION ON/OFF aroynd a code segment controls the how single floating point values are treated.
Tested with your Mandelbrot and there was a significant speedup.
Thanks for the benchmarks, could you try using the {$EXCESSPRECISION OFF} directive, the compiler will generate adds, mulss, subss, etc… and not do all the cvtss2sd and cvtsd2ss conversions.
That’s great, the {$EXCESSPRECISION OFF} directive seems to do the trick! It should be documented. For my “s1 := s1*1;” example it now correctly optimize away that line completely. Without the directive it inserts totally unnecessary conversion instructions for that line as described above.
This reminds me of the excessive code generation because of Delphi/C++ builder string compatibility a some years back that also could be turned off with a directive and thankfully was removed a few versions later.
Is there a way to set this directive for the whole project without having to add it in each unit?
@Allen B. Interesting Is this switch {$EXCESSPRECISION OFF} comparable to the fp:fast option in VS C/C++, in the sense of loosing correctness but more aggressive optimization … ?
2 links
http://msdn.microsoft.com/en-us/library/e7s85ffb%28VS.100%29.aspx
(Docu)
http://blogs.msdn.com/b/vcblog/archive/2009/11/02/visual-c-code-generation-in-visual-studio-2010.aspx
(Blog Post by the MS VC++ team)
Adding the directive at the top of the dpr seems to make it apply to the whole project. I wrote about this here: http://www.emix8.org/index.php?entry=entry110908-165856
This question that just came up on Stackoverflow shows that Visual Studio 2010 C-compiler do the same kind of code generation: http://stackoverflow.com/questions/7353681/can-this-c-loop-be-optimized-further
I take it all back, what I said except for the integer optimization, I’d like to see how the compiler does when it comes to MD5 hash and so, maybe there is another secret directive that optimizes it further, good job Embarcadero but why isn’t this documented anyway?.
The $EXCESSPRECISION Delphi compiler directive is now documented:
http://docwiki.embarcadero.com/RADStudio/en/Floating_point_precision_control_(Delphi_for_x64)
Thanks for all your comments here. If you want to comment on the compiler directive documentation, use the Discussion tab on the docwiki page.
The following msdn article gives some information about the MS VC++ compiler options:
http://msdn.microsoft.com/en-us/library/aa289157(v=vs.71).aspx
Btw, it has been suggested that this should be added as a project option, so I think that can be expected in a future release/update.
Here is the code that nothing will help.. freepascal x64 – 47ms, delphi x32 – 37ms, delphi x64 – 2.8s!!!, ms vs c++ x64 – 93ms
var
y, z: double;
i, x: integer;
t: Cardinal;
begin
write(‘Input X: ‘);
readln(x);
t := GetTickCount;
for i := 1 to 1000000 do
begin
y := i + (x / 2);
z := sin(sqr(y * 3));
end;
t := (GetTickCount – t);
Writeln(t);
Writeln(z);
Writeln(y);
readln;
end.